Revisit-DeepSeek-Key-Papers

From Llama-2 Replication to DeepSeek V3.2&R1: Revisiting DeepSeek’s 13 Research Papers for the Complete Technical Evolution of DeepSeek Base and Reasoning Models

Authors

Introduction

In Jan 2025, DeepSeek fundamentally reshaped the global AGI landscape with DeepSeek R1. But the R1 model didn’t appear out of nowhere. It was the culmination of a deliberate, methodical research trajectory spanning over a dozen papers — each one building directly on the innovations of the last. After R1, DeepSeek continued this trajectory with DeepSeek V3.2, DeepSeek Math V2, DeepSeek Prover V2, mHC, and Engram (As of Jan 2026).

After identifying and reading DeepSeek’s 13 papers, I realized that what makes DeepSeek remarkable is their culture and persuit for AGI. From the very beginning of DeepSeek LLM and DeepSeek MoE published in Jan 2024, DeepSeek wasn’t content to simply follow what others had done (e.g., Llama2 and Mistral). Instead, DeepSeek cultivated a different pursuit — not innovation for innovation’s sake, but a genuine drive to reduce costs and make things work better. They made bold bets, and as time went on, they diverged further and further from everyone else. By the time we look at these papers, DeepSeek had built their own distinct toolkit: GRPO, MLA, fine-grained shared MoE, DeepSeek Sparse Attention, mHC, and Engram.

Based on the 13 papers, this blog post traces DeepSeek’s complete technical evolution from Jan 2024 to Jan 2026 across two major arcs: 1) the base model lineage (DeepSeek LLM → MoE → V2 → V3 → V3.2) and 2) the reasoning model lineage (Coder → Math → Coder-V2 → Prover → Prover-V1.5 → R1 → Prover-V2 → Math-V2). What emerges is a story of incremental compounding — where each paper’s contribution, however modest in isolation, becomes a critical building block for what follows.

Overview

Overview of DeepSeek’s Research Trajectory

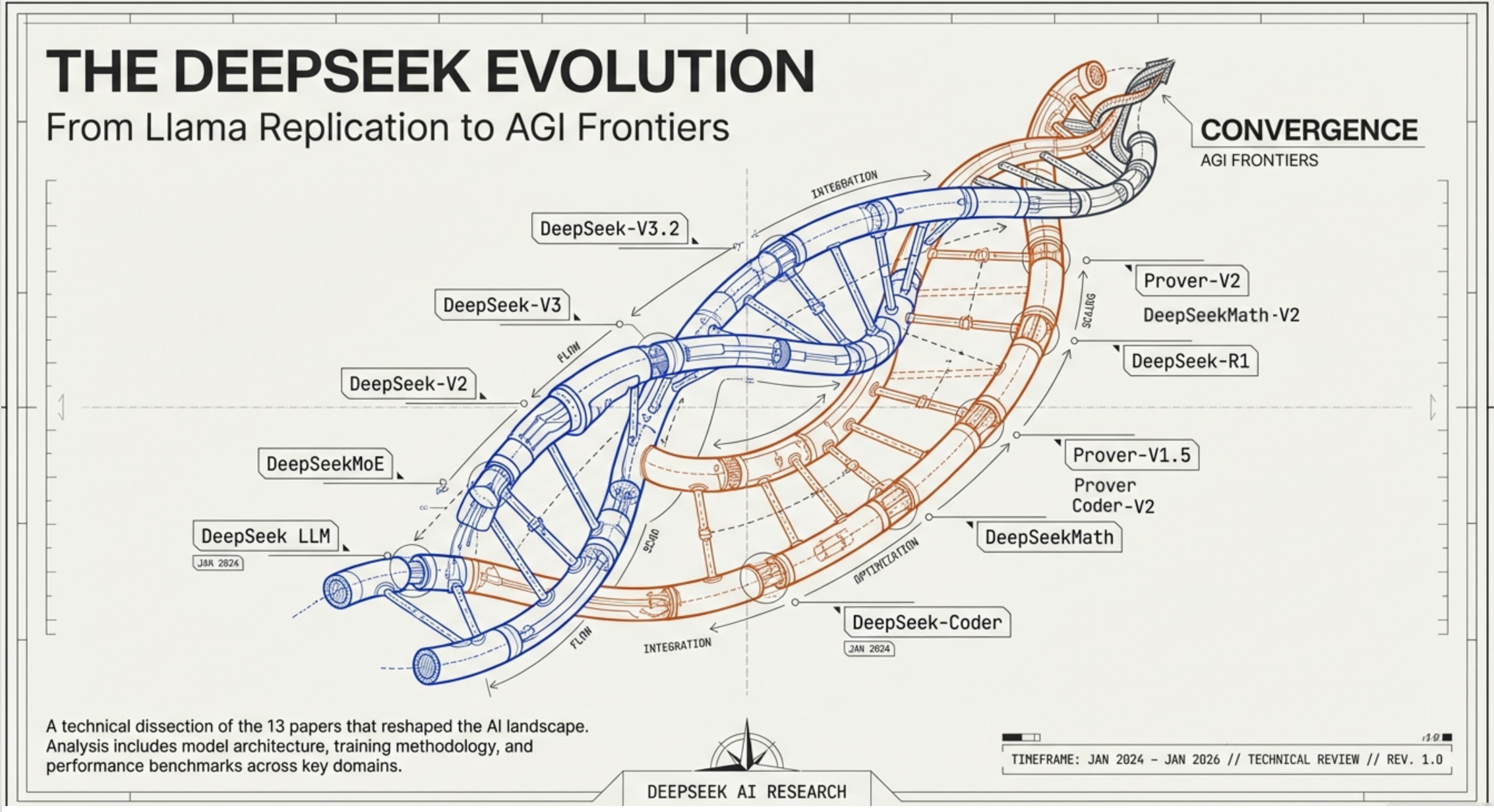
Overview Overview

Part I: Base Model Evolution

Paper 1 — DeepSeek LLM: Scaling Open-Source Language Models with Longtermism

The Starting Point: Scaling Laws Done Right

DeepSeek’s first LLM paper (January 2024) trained 7B and 67B parameter dense models. Architecturally, it follows the modern decoder-only transformer lineage (LLaMA-like design choices), but the paper’s core contribution is revisiting scaling laws — and this already revealed the “academic DNA” that would come to define DeepSeek.

The headline contribution wasn’t the models themselves — it was a rigorous set of scaling law experiments. While the community was familiar with the Chinchilla scaling laws from DeepMind, DeepSeek went further. They replaced approximate compute formulas with a more precise compute budget expression, used non-embedding FLOPs/token as the model scale representation, modeled scaling laws for hyperparameters (batch size, learning rate) as power laws against compute budget, and investigated how data quality impacts the optimal configuration of model size versus data volume.

The practical value of good scaling laws is enormous: they allow you to run small, cheap experiments and then accurately predict what generalization behavior you’ll achieve at any given training budget — before committing the compute. Using IsoFLOP profiling with their more precise compute formulation, DeepSeek’s scaling laws were precise enough that small-scale experiments could accurately forecast the expected loss of their 7B and 67B models. This kind of predictive capability is something few labs had demonstrated at the time, and it reflects an investment in understanding the science behind training that would pay dividends throughout DeepSeek’s entire research trajectory.

A particularly telling detail about DeepSeek’s culture: the paper explicitly emphasized avoiding “benchmark decoration” — the kinds of tricks commonly used across the industry to inflate evaluation scores. They also documented that fine-tuning alone could improve task-specific scores by over 20 points on benchmarks like HumanEval and GSM8K, underscoring how misleading raw benchmark numbers can be without controlled comparisons. Rather than chasing inflated numbers, DeepSeek chose transparent, controlled evaluation methodology. This was a conscious choice to respect the community, and it’s a strong signal of the lab’s research integrity.

Key Takeaways:

Paper 2 — DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models

The First Bold Bet: Fine-Grained Shared Experts

The MoE paper, published in Jan 2024, marks the beginning of DeepSeek’s architectural divergence from the mainstream. While other MoE implementations (like Mistral’s Mixtral) used 8 to 16 experts, DeepSeek went to 64 — a dramatic increase that seemed counterintuitive at the time.

[External context, not from the paper:] The broader context is worth understanding: even before ChatGPT, there were widespread rumors that GPT-4 and GPT-3.5 were MoE models — which would explain how OpenAI could offer them at such low API prices. If GPT-4 were truly a dense 100B+ model, the inference costs at that time would have been prohibitive. These rumors were later substantiated through various channels, making MoE a natural architectural choice for any lab serious about cost-efficient deployment.

The core motivation was cost reduction through sparse activation. In a Mixture-of-Experts architecture, you have many “expert” feed-forward networks but only activate a small subset for each token. DeepSeek’s 16B parameter MoE model only activated about 2.8B parameters per token, delivering dense-model-level quality at a fraction of the compute cost.

The paper introduced two key innovations:

Fine-Grained Expert Specialization: By using far more experts than the norm (64 instead of 8-16), each expert could specialize on narrower aspects of the data. Think of it as the difference between having 8 generalist doctors versus 64 specialists — the specialists can develop deeper expertise in their domains.

Shared Experts: DeepSeek introduced the concept of “shared experts” — a subset of experts that are always activated regardless of routing decisions. These shared experts capture common knowledge that every token needs access to, while the routed experts handle specialized knowledge. This was a novel and elegant solution to the problem of expert redundancy.

There’s also a practical advantage of the MoE architecture that’s often overlooked: MoE models are naturally suited for distributed computing. Since different experts can be placed on different GPUs, parallelization is straightforward compared to dense models, where splitting layers across devices is less intuitive. This property would become increasingly important as DeepSeek scaled to thousands of GPUs.

The paper validated these ideas at 2B and 16B scale, and partially trained a 145B model that showed promising results. But the real payoff would come in V2 and V3.

Key Takeaways:

Paper 3 — DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model

The Breakthrough: MLA and the Price War

Released in May 2024, V2 is where DeepSeek transformed from an interesting research lab into a force that disrupted the entire LLM market. This paper is the inflection point.

V2 scaled up to 236B total parameters with only 21B activated per token. That means it was a much larger model than the previous 67B dense model, yet cheaper to deploy. How was this possible?

Multi-head Latent Attention (MLA) — The Crown Jewel Innovation

The most significant technical contribution of V2 was MLA (Multi-head Latent Attention), a novel attention mechanism that dramatically reduced the KV (key-value) cache — the memory bottleneck during inference.

In standard multi-head attention, you need to store K and V vectors for every attention head across every layer for every token in the sequence. This KV cache grows linearly with sequence length and becomes the primary memory bottleneck during inference. Grouped Query Attention (GQA), used in models like Llama 2, partially addresses this by sharing K/V across groups of heads, reducing the cache by a factor of the group size.

DeepSeek’s MLA takes a fundamentally different approach. Instead of sharing K/V vectors across heads, MLA compresses keys and values into a latent vector using a low-rank projection. During inference, only these compressed latent vectors need to be cached. Attention can be computed directly from the cached latent representation and associated projections, without explicitly materializing full per-head K/V — sharply reducing KV-cache storage.

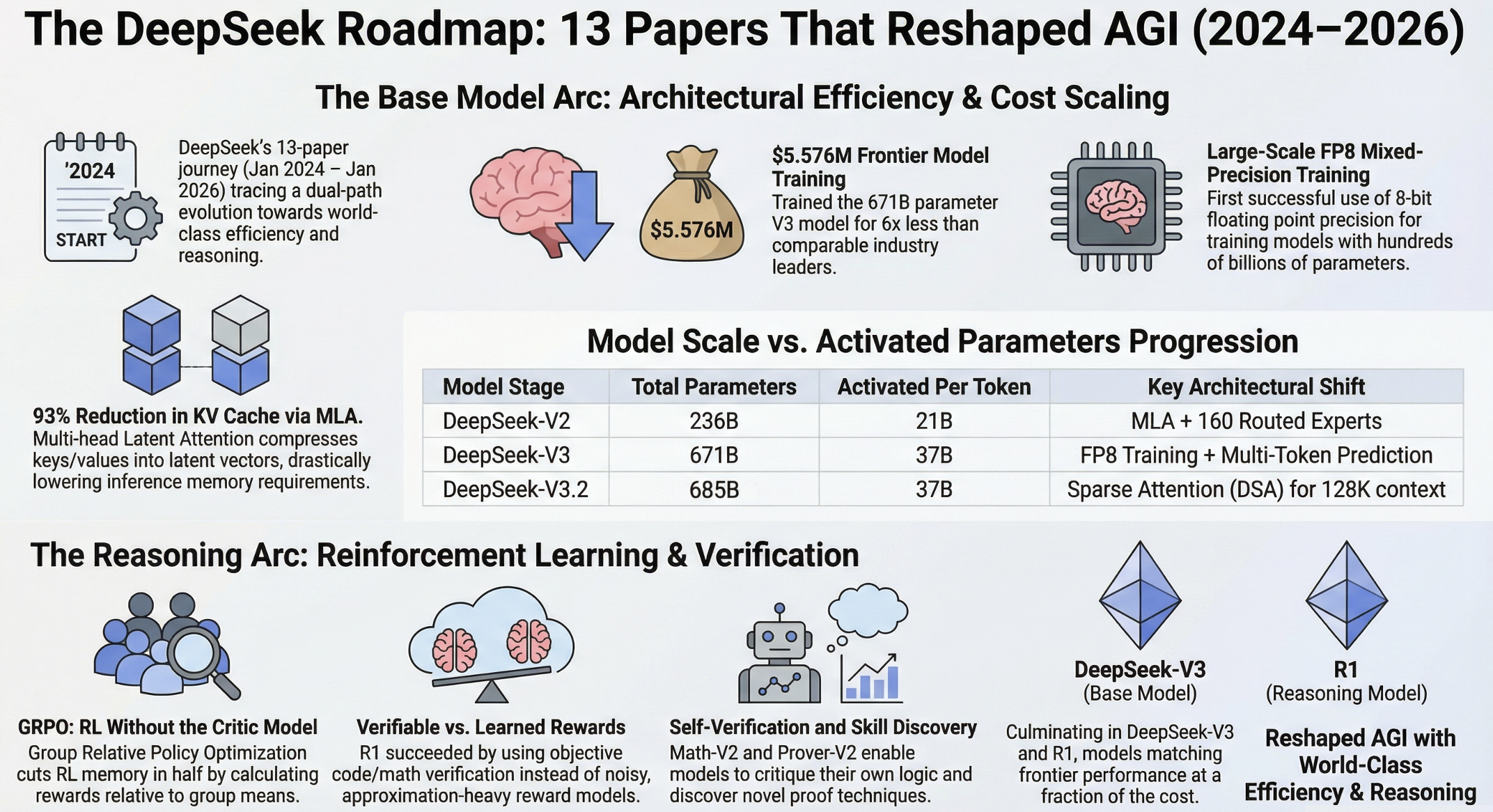
Walking through the math: the compression is equivalent to reducing the KV cache to roughly 2.25 GQA groups — a 93.3% reduction in KV cache compared to standard multi-head attention. The genius is that this compression happens in a learnable way, so the model learns the optimal way to compress its attention patterns.

Scaled MoE Architecture

V2 also scaled up the MoE architecture from the previous paper DeepSeekMoE: each MoE layer uses 2 shared experts and 160 routed experts, activating 6 routed experts per token (plus both shared experts). Scaling from 64 to 160 routed experts required solving significant engineering challenges around load balancing — ensuring that tokens are evenly distributed across experts and across different GPUs. Uneven distribution means wasted compute on underutilized GPUs. DeepSeek developed device-limited routing and explicit auxiliary losses for expert, device, and communication load balancing.

Market Impact: The API Price War

[Note: The following market observations are based on external reporting, not the V2 paper itself.] The paper is notable for an understated but seismic consequence: DeepSeek-V2 was so efficient to deploy that when they offered API access, they triggered a LLM price war. The per-million-token price was reportedly around one yuan (roughly $0.14) — far cheaper than OpenAI and several times cheaper than domestic competitors. The low cost was a genuine reflection of the MLA + MoE architecture’s efficiency.

When competitors tried to match DeepSeek’s prices, some may have been doing so at a loss. The shock to the industry was the realization that architectural innovation could translate directly into dramatic cost advantages.

Post-Training: SFT + RL with GRPO

The V2 paper describes a full post-training pipeline, more thorough than is sometimes appreciated. After SFT on 1.2M instruction-response pairs, V2 applies RL using GRPO in a two-stage strategy: first reasoning alignment (using code and math reward models), then human preference alignment (using helpful, safety, and rule-based reward models). This two-stage RL approach represents a deliberate and structured effort at alignment — not an afterthought. Nevertheless, DeepSeek’s broader culture remained research-first: the infrastructure costs were so low that the barrier to deployment was negligible, and V2’s real significance was its architectural innovations rather than its product polish.

Key Takeaways:

Paper 4 — DeepSeek-V3 Technical Report

The Engineering Marvel: $5.576M to Train a Frontier Model

V3, released in December 2024, represents the culmination of every innovation from the previous papers — and several new ones. This paper marked a shift in style: while previous papers felt like academic publications, V3 included over 10 pages of infrastructure documentation, reflecting the massive engineering effort involved. The infrastructure section is outside the scope of this post, but the engineering is clearly of exceptional quality.

The headline numbers: 671B total parameters, 37B activated per token, trained on 14.8 trillion tokens using only 2,048 H800 GPUs — notably, not the more powerful H100s. The export restrictions limited DeepSeek to H800s, which are less capable cards. Total training cost: approximately $5.576 million (assuming $2/GPU-hour rental price), covering pre-training, context extension, and post-training — though excluding earlier research and ablation costs. For comparison, training Llama 3.1’s 400B model reportedly cost $30 million or more — at least 6x the cost for a smaller model. This comparison, when it became public, shocked the industry and began to attract serious attention from American AI labs to DeepSeek’s technical innovations — particularly MLA and the MoE architecture from V2, which had previously been largely ignored outside China.

Training Stability: Zero Rollbacks

One extraordinary claim in the paper: the entire training run completed without a single rollback. In large-scale LLM training, it’s extremely common for training to diverge or encounter instabilities requiring checkpoints to be restored and training restarted — sometimes repeatedly. DeepSeek achieved a single continuous run from start to finish — a testament to both their infrastructure engineering and their understanding of training dynamics.

Multi-Token Prediction (MTP)

V3 adopted Multi-Token Prediction, where the model predicts one additional token beyond the standard next-token target (2 tokens total), using a 1-depth MTP module appended to the main model. The MTP framework is general and supports D sequential prediction modules, but V3 uses D=1. This technique, adapted from a recent research paper (not a DeepSeek original), served two purposes:

First, better representation learning: predicting the additional future token forces the model to develop richer internal representations, as it needs to capture longer-range dependencies. In practice, they found that even if you only use single-token prediction at inference time, the model trained with MTP performs better.

Second, speculative decoding during inference: the MTP head gives the model the ability to draft a second token in parallel. The paper reports approximately 85–90% acceptance rate for the second token and ~1.8× decoding throughput (tokens per second) when used for speculative decoding. This can significantly accelerate inference speed, breaking the inherent bottleneck of autoregressive generation where each token must be produced sequentially.

FP8 Mixed Precision Training

Perhaps the most technically daring innovation in V3 was the successful use of FP8 (8-bit floating point) for large-scale training. Previous LLM training had standardized on FP16 or BF16 (16-bit) precision. While FP8 quantization was common for inference deployment, nobody had successfully used it at scale during training.

Training in FP8 halves memory requirements and dramatically reduces compute costs, but the reduced numerical precision can cause training instability or degraded model quality. DeepSeek’s approach required careful study (“careful investigation,” as the paper puts it) of which operations need higher precision and which can safely be performed in FP8. They developed a mixed-precision strategy where most operations use FP8 but critical accumulations and certain intermediate variables maintain higher precision to keep training stable. This was the first successful deployment of FP8 training at the scale of hundreds of billions of parameters — another “bold bet” that paid off handsomely in cost reduction.

Refined MoE: 256 Experts with Auxiliary-Loss-Free Load Balancing

V3 scaled up to 1 shared expert plus 256 routed experts, with top-8 activation (8 routed experts activated per token plus the shared expert). Notably, they also changed the load balancing approach. Previous models used explicit auxiliary losses to encourage even token distribution across experts. V3 instead used an auxiliary-loss-free strategy with dynamic bias terms for routing — a more elegant solution that avoids the tension between the main training objective and the load balancing objective. They still employ a complementary sequence-wise balance loss to prevent extreme imbalance within a sequence, but the primary balancing mechanism no longer fights the training loss.

Key Takeaways:

Paper 5 — DeepSeek-V3.2: Pushing the Frontier of Open Large Language Models

The DeepSeek-V3.2 was released in Dec 2025. V3.2 is the direct architectural successor to V3, built via continued training from V3.1-Terminus, and represents the natural continuation of the base model lineage. The paper diagnoses three root causes for the gap between closed-source and open-source models: architectural inefficiency with vanilla attention at long contexts, insufficient computational investment during post-training, and weak generalization in agentic scenarios. V3.2 is their systematic attempt to address all three.

DeepSeek Sparse Attention: The Next Architectural Innovation

The first major contribution is DeepSeek Sparse Attention (DSA), a new attention mechanism that follows the same design philosophy as MLA — achieve comparable or better quality at dramatically lower cost, this time targeting the quadratic scaling of attention with sequence length.

The core idea is a two-component system: a “lightning indexer” and a fine-grained token selection mechanism. For each query token, the lightning indexer rapidly scores all preceding tokens to determine which ones are most relevant. Then, only the top-k key-value entries (where k = 2048 — far less than the full 128K context) are actually used for attention computation. This reduces the core attention complexity from O(L²) to O(L·k), where k is much smaller than L.

The lightning indexer itself is designed for extreme efficiency. It uses a small number of heads, ReLU activation (chosen specifically for throughput), and can be implemented in FP8. While the indexer still technically has O(L²) complexity, it’s so lightweight compared to full MLA that the end-to-end speedup is substantial — especially at long contexts where costs stay nearly flat for V3.2 while climbing steeply for V3.1.

How they integrated DSA into an already-trained model is noteworthy. Rather than training from scratch, DeepSeek continued training from their existing V3.1-Terminus checkpoint — a practical decision that reflects their characteristic incrementalism. The continued pre-training happens in two stages: first, a dense warm-up stage (just 2.1B tokens, ~1000 steps) where only the lightning indexer is trained using a KL-divergence loss to align its outputs with the existing attention distribution; then, a sparse training stage (943.7B tokens, ~15,000 steps) where the full model adapts to the sparse attention pattern. The indexer’s training signal is kept entirely separate from the language modeling loss — a clean architectural separation that prevents the indexer from disrupting the model’s learned representations.

Parity evaluations confirm that DSA preserves model quality: DeepSeek-V3.2-Exp (the base checkpoint with DSA) matches DeepSeek-V3.1-Terminus on standard benchmarks, human preference evaluations (ChatBot Arena Elo scores are closely matched), and independent long-context evaluations. The model actually scores higher on some long-context benchmarks like AA-LCR and Fiction.liveBench, suggesting DSA may slightly improve long-context reasoning while being substantially cheaper.

Scaling RL: Making RL Stable at Scale

If DSA is the architectural innovation of V3.2, the reinforcement learning scaling is the training innovation. V3.2’s post-training computational budget exceeds 10% of the pre-training cost — an extraordinary figure when most open-source models invest less than 1% in post-training. This level of RL compute only works if training is stable, and the paper details four specific techniques they developed to achieve this stability:

Unbiased KL Estimation. The standard K3 estimator for KL divergence, widely used in RLHF literature, turns out to have a biased gradient. When sampled tokens have substantially lower probability under the current policy than the reference policy, the K3 estimator assigns disproportionately large, unbounded weights — creating noisy gradient updates that accumulate and degrade sample quality in subsequent iterations. DeepSeek derives a corrected estimator using the importance-sampling ratio between current and old policies, yielding an unbiased gradient. This seemingly small mathematical fix eliminates a systematic error that compounds over thousands of training steps.

Off-Policy Sequence Masking. Large-scale RL systems typically generate large batches of rollout data split into mini-batches for multiple gradient updates, which introduces off-policy behavior. Additionally, inference frameworks optimized for speed may differ in implementation details from training frameworks, further widening the gap between sampling and training distributions. DeepSeek addresses this by measuring KL divergence between the data-sampling policy and the current policy for each sequence, and masking out negative-advantage sequences that exceed a divergence threshold. The intuition is that the model learns most from its own mistakes, but highly off-policy negative examples can mislead or destabilize optimization.

Keep Routing. This addresses an MoE-specific instability. In MoE models, different experts activate for different tokens, but discrepancies between inference and training frameworks — compounded by policy updates during RL — can cause inconsistent expert routing for identical inputs. This induces abrupt shifts in the active parameter subspace and destabilizes optimization. DeepSeek’s solution: preserve the exact expert routing paths from sampling and enforce them during training. This was found crucial for RL training stability in MoE models and has been used in their pipeline since DeepSeek-V3-0324.

Keep Sampling Mask. Top-p and top-k sampling improve generation quality but create a mismatch between the action spaces of the old and current policies, violating importance sampling assumptions. DeepSeek preserves the truncation masks from sampling and applies them identically during training, ensuring both policies operate on the same action subspace. This combination with top-p sampling also helps preserve language consistency during RL.

These four techniques collectively enable DeepSeek to push RL compute far beyond what was previously feasible for open-source models. The paper notes that different domains benefit from varying strengths of KL regularization — for mathematics, a weak or even zero KL penalty works best, while other domains need stronger regularization.

Specialist Distillation: Divide and Conquer

V3.2’s post-training pipeline uses a “specialist distillation” approach. For each of six specialized domains — mathematics, programming, general logical reasoning, general agentic tasks, agentic coding, and agentic search — DeepSeek trains a dedicated specialist model through large-scale RL. Each specialist is fine-tuned from the same V3.2 base checkpoint, and all domains support both “thinking” (chain-of-thought reasoning) and “non-thinking” (direct response) modes, with different models generating training data for each mode.

Once specialists reach peak domain performance, they generate high-quality domain-specific data, which is then combined and distilled into a single final checkpoint. This distilled model performs only marginally below the individual specialists, and the remaining gap is closed through subsequent mixed RL training that combines reasoning, agent, and human alignment objectives in a single stage — avoiding the catastrophic forgetting problems that plague multi-stage training pipelines.

Thinking in Tool-Use: The Agent Evolution

Perhaps the most forward-looking contribution is V3.2’s approach to integrating reasoning with tool use — representing the natural next frontier beyond the pure reasoning capabilities of R1.

DeepSeek identified a key inefficiency in simply applying R1’s reasoning approach to tool-calling scenarios: R1 discards reasoning content when new messages arrive, which forces the model to re-reason the entire problem from scratch after every tool call. V3.2 introduces a refined context management: historical reasoning content is only discarded when a new user message arrives, not when tool results come back. Tool call history and results are always preserved. This simple change dramatically reduces redundant computation in multi-turn tool interactions.

The cold-start mechanism bootstraps tool-use reasoning by combining existing reasoning data (non-agentic) with non-reasoning agentic data through carefully designed system prompts. This gives the model an initial — if imperfect — ability to generate reasoning-with-tool-use trajectories, which then provides the foundation for large-scale RL.

The scale of their agentic task synthesis is impressive: over 1,800 distinct environments and 85,000 complex prompts spanning four categories — search agents (50K+ tasks using real web search APIs), code agents (24K+ tasks from mined GitHub issue-PR pairs with real executable environments), code interpreter agents (6K tasks using Jupyter Notebooks), and general agents (4K+ tasks with automatically synthesized environments and toolsets). Importantly, the search and code environments are real — actual web APIs and actual executable code repositories — even though the prompts are synthetically generated or extracted.

The general agent synthesis pipeline is particularly clever: an automated agent creates task-oriented environments by generating databases, synthesizing tool functions, and then iteratively creating tasks of increasing difficulty — each with a solution function and verification function that ensures the task can only be solved through the tool interface, not by directly accessing the database.

V3.2-Speciale: Pushing the Reasoning Ceiling

To investigate the limits of extended thinking, DeepSeek developed V3.2-Speciale — a variant trained exclusively on reasoning data with a reduced length penalty during RL, allowing the model to think longer. The results are striking: V3.2-Speciale achieves gold-medal performance in the 2025 International Mathematical Olympiad (IMO), the International Olympiad in Informatics (IOI 2025), the ICPC World Finals 2025, and the China Mathematical Olympiad (CMO 2025). It achieves performance parity with Gemini-3.0-Pro, the leading closed-source system.

There’s a trade-off, however, that the paper is transparent about: V3.2-Speciale uses significantly more tokens than Gemini-3.0-Pro to reach similar performance levels. On AIME 2025, Speciale averages 23K output tokens versus Gemini’s 15K. On Codeforces, the gap is even larger: 77K versus 22K. The model achieves comparable accuracy but at higher token cost — a token efficiency problem the paper acknowledges as a key direction for future work.

Limitations and Lessons

The paper’s conclusion is notable for its intellectual honesty. Three limitations are explicitly acknowledged: first, world knowledge remains limited due to fewer total training FLOPs — the gap between open-source and closed-source pre-training budgets directly translates into a knowledge gap. Second, token efficiency is still a challenge — V3.2 typically requires longer generation trajectories to match the output quality of models like Gemini-3.0-Pro, and future work will focus on improving the “intelligence density” of reasoning chains. Third, performance on the hardest tasks still trails frontier models.

But perhaps the most resonant insight comes in the paper’s final framing: if Gemini-3.0-Pro proves the potential of continued pre-training expansion, then DeepSeek-V3.2-Speciale proves the scalability of reinforcement learning in a large-scale context. The implication is clear: closed-source labs have the resources to stack pre-training compute, but open-source can find an alternative path — through more efficient architecture and more scientific post-training.

Key Takeaways:

Part II: Reasoning Model Evolution

The second major arc of DeepSeek’s research is the reasoning model lineage — the work that ultimately produced R1, the model that shook the AI world in Jan 2025. This arc traces a progression from code intelligence to formal mathematics to general reasoning, where each step built the foundations for the next. Notably, many of the RL techniques refined in this lineage (especially GRPO) would later be scaled up dramatically in V3.2’s post-training.

Paper 6 — DeepSeek-Coder: When the Large Language Model Meets Programming — The Rise of Code Intelligence

Building the Code Foundation

In Jan 2024, DeepSeek-Coder introduced a family of code models (1.3B to 33B parameters) trained from scratch on 2 trillion tokens of code data. The paper’s significance lies in establishing the code pre-training infrastructure and data pipeline that would underpin DeepSeek’s entire reasoning model lineage.

The key technical contributions were in data and training methodology rather than algorithmic innovation. DeepSeek-Coder used repository-level data organization — instead of treating code files as independent documents, the training data preserved the dependency structure of entire repositories, allowing the model to learn cross-file relationships (imports, function calls, class hierarchies). This is a crucial distinction from simply training on a bag of code files.

The paper also employed Fill-In-Middle (FIM) style training — in addition to standard left-to-right language modeling, the model was trained to fill in missing code segments given surrounding context. This bidirectional capability is essential for practical code tasks like code completion, where the model needs to understand both what comes before and after the insertion point. The models supported a 16K context window.

Why does a code pre-training paper matter for the reasoning story? Because DeepSeek-Coder-Base-v1.5 — the base model produced by this line of work — became the foundation on which DeepSeekMath (Paper 7) was built. The hypothesis, later validated, was that code pre-training develops structured reasoning capabilities (planning, logic, compositional thinking) that transfer well to mathematical reasoning. This code → math pipeline became a defining feature of DeepSeek’s approach.

Key Takeaways:

Paper 7 — DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

Where GRPO Is Born

DeepSeekMath is the paper that introduces Group Relative Policy Optimization (GRPO) in Feb 2024, which provides the theoretical foundation that later powers R1, V2’s RL stage, and V3.2’s post-training. To understand GRPO, it helps to understand the problem it solves. Standard PPO (Proximal Policy Optimization), the dominant RL algorithm for LLM training, requires four separate models during training: the policy model (being trained), a reward model (judging quality), a reference model (preventing drift), and a value/critic model (estimating expected returns for baseline computation). Each model is roughly the same size as the policy model itself, making PPO extremely resource-intensive.

GRPO’s key innovation is eliminating the critic/value model. Instead of training a separate model to estimate baselines for advantage computation, GRPO samples a group of outputs for each question, obtains rewards for each (from whatever reward source is available — a learned reward model, or rule-based rewards for verifiable tasks), and uses the group mean of rewards as the baseline. Each output’s advantage is computed relative to that group mean. This is conceptually simple but practically transformative — it cuts RL training memory roughly in half while maintaining or improving performance.

An important distinction: GRPO eliminates the value model, not the reward model. It still requires a reward signal, which can come from either a learned reward model or rule-based verification. In DeepSeekMath itself, GRPO is explicitly paired with learned reward models. The later choice to use rule-based rewards (as in R1-Zero) is a separate, orthogonal design decision about the reward source — not a property of GRPO itself. DeepSeekMath also introduces iterative GRPO, where the reward model is periodically retrained on the policy model’s latest outputs, preventing the reward signal from going stale as the policy improves.

The paper builds DeepSeekMath 7B by continuing pre-training DeepSeek-Coder-Base-v1.5 7B with 120B math-related tokens from Common Crawl — a deliberate choice that validates the hypothesis that code training provides a strong foundation for mathematical reasoning.

The other major contribution is the data pipeline: rather than relying on arXiv papers (which the authors find provide limited benefit for math reasoning — a counterintuitive result), they build an iterative fastText-based classifier that mines high-quality math content from Common Crawl. Starting from OpenWebMath as a seed corpus, each iteration trains a classifier, retrieves more math pages, and refines with human annotation. The resulting 120B-token DeepSeekMath Corpus is significantly larger and more diverse than existing math datasets.

A key analytical insight: the paper provides a unified framework showing that SFT, rejection sampling (RFT), DPO, PPO, and GRPO can all be understood as points on a spectrum of direct-to-simplified RL. Under this lens, GRPO’s advantage becomes clear — it captures most of PPO’s online learning benefits while being nearly as simple to implement as DPO. The results confirm this: DeepSeekMath-RL 7B achieves 51.7% on the competition-level MATH benchmark (approaching GPT-4) and 88.2% on GSM8K, with self-consistency over 64 samples reaching 60.9% on MATH.

One subtle finding: GRPO improves Maj@K (majority voting accuracy) substantially but has minimal effect on Pass@K (whether any sample is correct). This reveals that RL doesn’t teach the model new capabilities — it makes existing capabilities more reliable by increasing the probability of correct reasoning paths. This observation foreshadows R1’s approach: RL as a way to sharpen and surface reasoning abilities that are already latent in the base model.

Key Takeaways:

Paper 8 — DeepSeek-Coder-V2: Breaking the Barrier of Closed-Source Models in Code Intelligence

Matching Closed-Source Performance on the V2 Architecture

Coder-V2 represented a significant leap: an open-source code model that matched or exceeded closed-source models (notably GPT-4 at the time) on coding benchmarks. This paper was significant not just for its results but for demonstrating that the V2 architecture (MLA + MoE) could be effectively adapted for specialized domains.

Built upon an intermediate checkpoint of DeepSeek-V2, Coder-V2 was continued pre-training on an additional 6 trillion tokens, reaching a total exposure of 10.2 trillion tokens and expanding to 338 programming languages with 128K context support. The models come in 16B and 236B variants, with 2.4B and 21B activated parameters respectively. This was substantially more than a fine-tuned V2 — it involved extensive additional pre-training with careful data mixing strategies to maintain general capabilities while building deep code understanding.

The paper uses GRPO for RL alignment after SFT, with preference data and reward models. Notably, the paper’s internal experiments suggest that reward-model-guided RL can outperform raw compiler pass/fail feedback in certain settings — a finding that complicates any simple narrative of “reward models don’t work.” Later DeepSeek papers would explore rule-based and other reward sources more aggressively, but Coder-V2 itself found reward models beneficial in the RL stage.

Key Takeaways:

Paper 9 — DeepSeek-Prover: Advancing Theorem Proving in LLMs through Large-Scale Synthetic Data

From Code to Formal Mathematics — Verifiable Rewards Without RL

DeepSeek-Prover moved into formal theorem proving — a domain deeply connected to the eventual R1 approach. The key insight is that formal mathematics, like code, has a built-in verification mechanism.

The paper focuses on scaling theorem proving via synthetic Lean 4 datasets. The pipeline works as follows: natural-language competition problems are translated into formal Lean 4 statements, statements are filtered for quality, and proofs are generated — creating a very large synthetic corpus. DeepSeekMath 7B is then fine-tuned on a dataset of 8 million formal statements with proofs. Lean serves as a theorem-proving engine — essentially a “compiler” for mathematics. You give it a proof in its formal language, and it tells you definitively whether the proof is valid. This is analogous to how code can be verified by running test cases: the reward signal is rule-based and doesn’t require a separate model to judge correctness.

The connection to R1 is worth emphasizing: like math answer checking and code test cases, Lean provides a verifiable reward signal that doesn’t depend on a learned reward model. This is the same principle that would later drive R1’s success.

However, Prover V1 did not yet use reinforcement learning. Instead, it used iterative self-improvement (rejection sampling): the model generates formal proofs, Lean verifies them, incorrect proofs are discarded, correct proofs are kept for further training, and the process repeats. DeepSeekMath had already begun to show that online RL (GRPO) could outperform such offline approaches for reasoning — setting the stage for Prover-V1.5 to adopt RL.

The paper’s other major contribution was large-scale synthetic data generation for formal mathematics. Training data for theorem proving is extremely scarce — there are far fewer formal proofs than code repositories. DeepSeek addressed this by developing methods to generate synthetic proof data at scale.

Key Takeaways:

Paper 10 — DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search

The RL Bridge to R1

Prover V1.5, published in August 2024, is where the reasoning model thread gets really interesting. This paper made the natural transition from the iterative self-improvement of Prover V1 to full online RL — building on DeepSeekMath’s demonstration that GRPO could improve reasoning performance.

The paper uses GRPO (from DeepSeekMath) with Lean’s proof verification as the reward signal, and introduces RMaxTS, a Monte-Carlo Tree Search variant for exploring diverse proof paths. But it faced a critical challenge: reward sparsity. While Lean can tell you definitively whether a proof is correct, formal proofs are difficult — the model often fails to produce any correct proof at all, meaning the reward signal is overwhelmingly negative. This is much sparser than, say, math problems where the model might get 30-50% correct.

DeepSeek’s pragmatic solution was to remove the hardest problems from the training set — those where the model couldn’t produce any correct proofs. By focusing RL training on problems at the boundary of the model’s capability, they ensured a meaningful reward signal. Notably, they did not train a separate reward model to address the sparsity problem. This can be seen as an early sign of DeepSeek’s gradual shift away from learned reward models — they chose to work within the constraints of rule-based verification rather than adding model complexity.

The paper also experimented with Monte-Carlo Tree Search (MCTS) at inference time, developing a variant called RMaxTS. This involved building a search tree where the model explores multiple proof strategies, using Lean feedback to guide the search. The MCTS results were strong, and at the time, there was significant community speculation that OpenAI’s o1 might use similar tree search techniques. As it turned out, this speculation was likely wrong — but the exploration was valuable research nonetheless.

Key Takeaways:

Paper 11 — DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning

The Paper That Changed Everything

R1 is where everything comes together. To understand why R1’s approach works, it helps to look at what the broader research community was trying at the same time — and why those attempts failed.

The Community’s Convergence

[Note: The following discussion of community efforts to replicate o1 draws on external reporting and accounts from multiple research groups — it is not sourced from the R1 paper itself, which focuses on DeepSeek’s own technical contributions.]

A fascinating story of independent convergence unfolded across the research community. After OpenAI released o1 (September 2024), many research groups tried to replicate it:

Phase 1: The Reward Model Approach (Failed). Following what many assumed was OpenAI’s approach (influenced by OpenAI’s process supervision paper), multiple research teams initially tried building reward models to guide RL training. They used open-source process reward models (from Math-Shepherd / DeepSeek’s own earlier work) to do online PPO for math reasoning. After 2-3 months of effort, the consensus was that this approach was fundamentally difficult — the reward model quality wasn’t sufficient to reliably guide reasoning improvement. No matter how they tuned it, PPO with reward models just wouldn’t work.

Phase 2: Iterative Self-Improvement (Worked, but Limited). After abandoning the reward model approach, they pivoted to iterative self-improvement — essentially rejection sampling SFT, where the model generates multiple solutions, correct ones are kept for further training, and the process repeats. This was the mainstream approach in the community at the time (also used by Llama 3’s post-training). This worked, and they completed this project successfully. But they realized the approach had a ceiling — it’s offline, and their earlier work (and DeepSeek-Coder’s findings) suggested online RL should be better.

Phase 3: Online RL Without Reward Models (The Answer). Finally, by late 2024, they returned to online RL (PPO/GRPO-style) — but this time without a learned reward model. Instead of a reward model, they used verifiable signals: for math problems, check if the answer is correct; for code, check if it passes test cases. This worked dramatically well, in stark contrast to their earlier failed attempts with reward models.

The remarkable thing is that multiple teams independently converged on this same insight around the same time: you don’t need reward models for reasoning. Verifiable rewards are sufficient, and they’re actually better because they provide ground-truth signal rather than a noisy approximation. Teams like Kimi (which released K1.5) arrived at the same approach independently.

R1-Zero: The Surprising Experiment

One of the most impressive results in the R1 paper is R1-Zero — a model that skips supervised fine-tuning entirely and applies RL directly to the base model (V3). This was unexpected because every prior approach, including DeepSeek’s own earlier work, started with SFT to give the model initial reasoning patterns before applying RL. No one had tried going straight from a base model to RL, partly because the community assumed it wouldn’t work and partly because SFT was seen as necessary to bootstrap reasoning capabilities.

R1-Zero produced remarkable results: on AIME 2024, pass@1 scores climbed from 15.6% to 71.0%, with majority voting reaching 86.7%. The model’s chain-of-thought length grew steadily during training, and — perhaps most strikingly — the model began exhibiting self-reflection behaviors: re-examining its own reasoning, catching errors, and trying alternative approaches. Whether these capabilities were truly “emergent” from RL or merely “unlocked” from latent abilities in the base model remains an active research question, but the result was impressive nonetheless.

What’s genuinely surprising about R1-Zero is how well pure RL training without SFT worked — many researchers hadn’t expected this.

R1: The Full Pipeline

The production R1 model that users interact with includes an additional SFT “cold start” step before RL training. DeepSeek collects long chain-of-thought data (somewhat like distillation from their own models) and fine-tunes V3 on it, then applies RL. This SFT+RL combination produces even better results than R1-Zero alone.

An important nuance often lost in simplified accounts: R1 still uses reward models for non-verifiable tasks. For math (check the answer) and code (run test cases), rule-based rewards work perfectly. But for general-purpose tasks — creative writing, open-ended reasoning, instruction following — there are no simple rules to verify quality. For these domains, R1 does use reward models. The “no reward model” narrative applies specifically to the math and code reasoning that produces R1’s most impressive results.

The R1 Paper as “Culmination”

An interesting observation: R1 is paradoxically the simplest paper in the entire lineage. The base model (V3) was already built. GRPO was already invented and battle-tested. The architectural innovations (MLA, fine-grained MoE) were already validated. The insight that verifiable rewards work was already demonstrated in the Prover papers. R1 essentially combined existing pieces at scale — and the result was extraordinary. R1 “didn’t appear out of nowhere” — it was the culmination of all previous successful (and failed) work.

The OpenAI Misdirection

[Note: The following is external commentary based on public discussions, not sourced from DeepSeek papers.]

A provocative observation: OpenAI’s process supervision paper may have inadvertently misled the community for months. The story is worth telling in detail.

After OpenAI published their process supervision research (“Let’s Verify Step by Step”), the community became convinced that process reward models (PRMs) — models that judge whether each individual step in a reasoning chain is correct, not just the final answer — were the key to building reasoning models. OpenAI had invested heavily in this approach: they hired math professionals to manually label approximately 800,000 examples (the PRM800K dataset, still widely used today), where each step of a math solution was annotated as correct or incorrect. They then trained a model to predict step-level correctness.

This was enormously influential. The community largely assumed o1 must use process supervision, since OpenAI had published such prominent work on it. Math-Shepherd — an open-source effort connected to DeepSeek’s earlier work — was one of the first to replicate this pipeline without human annotation, automatically constructing step-level labels. Many researchers spent months building on this paradigm.

The problem? It didn’t work well for RL training. The fundamental issue can be illustrated with a vivid analogy: rule-based rewards are universal, but reward models are distribution-sensitive. Consider checking a math answer: the rule “final answer matches the solution” works identically whether the problem is elementary school arithmetic or doctoral-level analysis. The rule doesn’t care about difficulty. But a reward model trained on elementary and middle school math data may judge those problems accurately while failing completely on university-level problems. This is the generalization problem — reward models are inherently brittle when the RL training pushes the model beyond the reward model’s own competence boundary.

Later, OpenAI’s own technical staff indicated on social media that DeepSeek’s approach was likely similar to what o1 actually used — suggesting that the community’s earlier assumptions about o1’s architecture (based on the process supervision paper) may have been wrong. The PRM paper, it seems, described research OpenAI had explored but not necessarily the approach they ultimately used for o1.

The Nuance: Process Supervision’s Theoretical Ceiling

An important nuance that’s often lost in the “no reward model needed” narrative: rule-based rewards have a fundamental limitation — they only provide outcome-level feedback. For math, you know if the final answer is right or wrong, but you don’t know which step went wrong. For code, you know if the test passed or failed, but not which line caused the bug. This is a sparse reward signal.

If process reward models could be made to work reliably — providing dense, step-level feedback — the theoretical ceiling would be higher than outcome-only rewards. The problem isn’t that the idea of process supervision is wrong; it’s that in practice, building reward models good enough to provide reliable step-level judgments at scale remains extremely difficult. Rule-based rewards won pragmatically, not theoretically.

This same reward sparsity challenge extends to other potential RL domains. Consider autonomous driving as an example: you could design rule-based rewards (crashing = wrong, staying in lane = right, obeying traffic lights = correct), but these are extremely sparse — the car might drive for thousands of steps before encountering a reward-giving event. For domains with complex multi-step interactions, dense feedback would be far more useful, but we don’t yet know how to provide it reliably.

Key Takeaways:

Paper 12 — DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition

Note: This paper (April 2025) is the direct successor to DeepSeek-Prover-V1.5 and represents the convergence of the reasoning lineage (R1’s RL techniques) with the formal proving lineage.

Bridging Informal and Formal Reasoning

DeepSeek-Prover-V1.5 proved theorems by generating complete Lean 4 proofs in a single pass or via MCTS. Prover-V2 attacks a deeper problem: how to make a model reason informally (like R1) and then formalize that reasoning into machine-verified proofs. The core insight is that natural-language chain-of-thought and formal proof construction are complementary skills that can be unified in a single model — rather than treating them as separate tasks.

The key challenge is that LLMs reason informally through heuristics and approximations, while proof assistants like Lean demand every step be explicitly justified. Previous approaches like Draft-Sketch-Prove attempted to use proof sketches to guide formalization, but struggled with sparse training signals. Prover-V2 solves this through a recursive decomposition pipeline that generates dense, high-quality training data.

Recursive Subgoal Decomposition: The Data Engine

The cold-start data collection is the paper’s most creative contribution. DeepSeek-V3 (the general-purpose model) serves as both the high-level reasoner and the formalizer: it generates a natural-language proof sketch for a theorem while simultaneously decomposing it into a sequence of formal Lean subgoals with sorry placeholders. A smaller 7B prover model then recursively resolves each subgoal — handling the low-level proof search where brute computational effort matters more than high-level insight. When all subgoals are solved, their proofs are composed into a complete formal proof and paired with V3’s original chain-of-thought, creating a unified training example that connects informal reasoning to formal verification.

This division of labor — big model for strategy, small model for tactics — is computationally elegant. It also enables a curriculum learning framework: the decomposed subgoals themselves become a source of conjectural theorems of increasing difficulty, providing dense training signal rather than the sparse binary “proved/not proved” feedback that limited earlier approaches.

Two Modes, Two Stages

Prover-V2 trains through a two-stage pipeline producing two complementary modes. The first stage creates a high-efficiency non-CoT mode optimized for rapid formal proof generation — this is the workhorse for data collection and expert iteration cycles, where inference speed matters. The second stage builds a CoT mode that integrates V3’s informal reasoning patterns with formal proofs, then refines this through reinforcement learning following the standard reasoning model pipeline established by R1.

The 671B version is trained on top of DeepSeek-V3-Base (the same foundation as R1), while a 7B version extends DeepSeek-Prover-V1.5-Base with 32K context length — maintaining the “validate small, deploy large” pattern.

Results: Formal Reasoning Approaches Informal

The headline numbers represent a dramatic leap: 88.9% pass ratio on MiniF2F-test (up from V1.5’s 63.5%) and 49 out of 658 PutnamBench problems solved — undergraduate competition mathematics, formally verified. The paper also introduces ProverBench (325 formalized problems including 15 AIME problems), where Prover-V2 solves 6 out of 15 AIME problems via formal proofs. For comparison, DeepSeek-V3 solves 8 of the same problems informally via majority voting. The gap between “getting the right answer” and “constructing a machine-verified proof of the answer” has narrowed from a chasm to a crack.

An interesting finding from the RL stage: reinforcement learning enabled the model to discover novel proof techniques not present in its training data — what the authors call “skill discovery.” This echoes R1-Zero’s emergence of self-reflection: RL doesn’t just optimize within known strategies but can generate genuinely new approaches.

Key Takeaways:

Paper 13 — DeepSeekMath-V2: Towards Self-Verifiable Mathematical Reasoning

Note: This paper (November 2025) is built on DeepSeek-V3.2-Exp-Base and represents a fundamental shift from DeepSeekMath V1’s approach: instead of chasing correct final answers, it pursues correct reasoning — the ability to generate rigorous proofs and, crucially, verify their own validity.

The Problem with Correct Answers

DeepSeekMath V1 trained models to produce correct final answers via GRPO with outcome-based rewards: if the answer matched, the model was rewarded. This worked well for competition math — 51.7% on MATH — but it has two fundamental limitations that V2 confronts directly. First, correct answers don’t guarantee correct reasoning: a model can arrive at the right number through flawed logic or lucky cancellation of errors. Second, outcome rewards are inapplicable to theorem proving, where the task isn’t to produce a number but to construct a rigorous step-by-step derivation. You can’t verify a proof by checking whether it matches an “answer key.”

V2’s central thesis is that to push mathematical AI further — especially toward open problems with no known solutions — models need to verify the process, not just the outcome. This requires self-verification: the ability to critique and correct one’s own proofs without reference solutions.

The Verifier-Generator-Meta-Verifier Architecture

V2 introduces a three-layer system unlike anything in V1. The proof verifier is trained via GRPO to evaluate proofs against rubrics (scoring 0/0.5/1 for flawed/minor-issues/rigorous), with rewards based on how closely its predicted scores match expert annotations. But here’s the subtlety: a verifier optimized only on score accuracy can game the reward by hallucinating fake issues while still outputting the correct score. To catch this, V2 introduces a meta-verifier — a second model that evaluates whether the verifier’s identified issues actually exist and logically justify its score. The meta-verifier’s feedback is folded back into verifier training, improving the faithfulness (not just accuracy) of verification from 0.85 to 0.96 quality score.

The proof generator is then trained using the verifier as a generative reward model. The key innovation: during training, the generator must produce both a proof and a self-analysis following the same rubrics as the verifier. The reward function combines proof quality (scored by the verifier) with self-analysis quality (scored by the meta-verifier), creating an incentive to find and fix issues before finalizing. This is qualitatively different from R1’s approach: rather than blind trial-and-error against outcome rewards, the model explicitly understands its reward function and maximizes it through deliberate self-critique.

The Self-Improvement Cycle

The most elegant aspect of V2 is how verifier and generator co-evolve. As the generator improves, it produces proofs that are harder to distinguish — good enough to fool the current verifier. These challenging cases become training data for the next verifier iteration. The key question is: where does this new labeled data come from? Initially, human experts annotate. But by the last two training iterations, V2 replaces human annotation entirely with an automated pipeline: generate n independent verifier analyses per proof, meta-verify the ones that flag issues, and label based on consensus. Quality checks confirmed automated labels matched expert judgments.

This addresses a deep problem: scaling verification compute as a substitute for human annotation. If you can automatically label proofs that challenge your current verifier, you can bootstrap an improvement cycle without the annotation bottleneck that limits most RL approaches.

How It Differs from V1

The contrast with DeepSeekMath V1 is stark across every dimension. V1 was a 7B model continued from Coder-Base; V2 is built on DeepSeek-V3.2-Exp-Base (685B-scale). V1 optimized for final-answer accuracy on competition math; V2 optimizes for proof rigor on theorem proving. V1 used GRPO with outcome rewards (correct/incorrect answer); V2 uses GRPO with a learned verifier as the reward model, plus meta-verification for faithfulness. V1’s best result was 51.7% on MATH; V2 scores 118/120 on Putnam 2024 (surpassing the highest human score of 90), achieves gold-medal performance on IMO 2025 (5/6 problems), and CMO 2024. On one-shot generation across CNML-level problems, V2 outperforms GPT-5-Thinking and Gemini 2.5-Pro.

Sequential refinement with self-verification is another capability V1 lacked entirely. When V2 fails to produce a rigorous proof in one attempt, it can recognize this through self-analysis and iteratively refine across multiple attempts — a form of test-time compute scaling that depends on faithful self-assessment rather than just brute-force sampling.

Key Takeaways:

The DeepSeek DNA: Cultural and Organizational Observations

When reading the technical papers, I am also wondering what makes DeepSeek remarkable. The answer can be the organizational culture that produced them. Several patterns stand out when you look at the company from the outside.

Academic Rigor in an Industry Lab

DeepSeek’s papers read like university papers. They do detailed scaling law studies, ablation experiments, and transparent reporting — the kind of careful scientific work that industry labs often skip in favor of “bigger model, better benchmarks.” They have industry-level resources but approach problems with academic thoroughness. Their publication rate would be high even for academia (over a dozen significant papers in roughly two years), but the academic quality of each paper is what’s truly unusual.

The effect on the broader research community has been overwhelmingly positive. Unlike many companies that release models without explaining the science, DeepSeek’s papers actually help researchers understand what works and why — functioning more like university publications than corporate announcements. Even before R1 made them famous, DeepSeek had a strong reputation within the academic research community, even though the general public and tech media largely hadn’t heard of them.

Courage to Innovate at Scale

What truly distinguishes DeepSeek is their willingness to risk large-scale training on unproven techniques. Going to 160 experts when everyone used 8-16. Deploying MLA at 236B scale without validation at that size. Training a 671B model in FP8 when nobody had proven it works. Each of these was a multi-million dollar bet. Most companies would validate extensively before committing resources at that scale. DeepSeek placed the bets and won.

Innovation Categorization

What counts as “purely original” versus “engineering innovation”? Multiple algorithmic inventions stand out clearly, e.g., MLA and GRPO. But engineering innovations like fine-grained MoE, successful FP8 training at scale, and multi-token prediction deployment should also be considered creative contributions — even when the underlying concepts were proposed by others. Being the first to successfully deploy a technique at massive scale, and sharing the results, is its own form of innovation. This incremental accumulation of small innovations at each stage is exactly what created a “very innovative company” by the time V3 and R1 arrived — each generation only had one or two novel elements, but they compounded.

Cost-Consciousness as Innovation Driver

Their innovations weren’t for the sake of novelty — they were driven by a genuine need to reduce costs. The MoE architecture, MLA, FP8 training, GRPO — each innovation was motivated by making training and inference more affordable. This practical motivation produced innovations that turned out to be architecturally superior.

Conclusion: The Innovation Pattern

Looking across DeepSeek’s full publication history — thirteen papers spanning — a clear pattern emerges in their approach to innovation:

  1. Validate at small scale, then commit at large scale. From MoE (2B → 16B → 145B → V2 → V3) to MLA (validated in V2, scaled in V3), to DSA (validated against V3.1-Terminus, deployed in V3.2), they systematically de-risk novel ideas before making large commitments.

  2. Build incrementally on previous work. Each paper builds directly on the innovations of the last. MoE experts → shared experts in V2 → refined balancing in V3. MLA invented in V2 → refined in V3 → extended with DSA in V3.2. Code pre-training in Coder → foundation for DeepSeekMath → GRPO introduced in DeepSeekMath → applied in V2’s RL stage → applied to Prover V1.5 → applied to R1 → scaled with stability techniques in V3.2 → used to train verifier/generator in DeepSeekMath-V2. Outcome rewards (DeepSeekMath) → verifiable rewards (R1) → process verification with self-critique (DeepSeekMath-V2). And the lineages converge: Prover-V2 unifies formal proving with R1’s RL, while DeepSeekMath-V2 makes the generator its own verifier.

  3. Pursue engineering optimization alongside algorithmic advances. Novel architectures are paired with novel infrastructure — FP8 training, communication optimization, load balancing, keep routing for MoE RL stability, custom cluster management.

  4. Follow the cost gradient. Every major innovation reduces the cost of training or inference. This isn’t just thrift — it’s a strategic philosophy that compounds over time. MLA reduced KV cache by 93%. DSA reduced long-context attention from quadratic to near-linear. Each generation makes the next one cheaper.

  5. Maintain self-belief through the wilderness. GRPO and MLA were largely ignored by others for months. DeepSeek kept using them because the internal results justified it. This conviction — using their own tools even when the community hadn’t adopted them — turned out to be a major advantage.

  6. Be honest about limitations. From the first paper’s transparent benchmark reporting, DeepSeek consistently prioritizes intellectual honesty over PR narratives. This honesty builds trust in their actual achievements.

The result is a research trajectory that went from replicating Llama 2 in late 2023 to producing a model that rivaled the best in the world, achieves IMO gold, and can verify the rigor of its own proofs. Along the way, the formal proving lineage achieved its own milestone: machine-verified proofs of competition mathematics problems that nearly match what informal reasoning can solve. DeepSeek’s story isn’t just about any single technical innovation. It’s about what happens when academic rigor, engineering excellence, and a willingness to take calculated risks converge in an organization with the patience to let good research compound.

Appendix: Paper References

  1. DeepSeek LLM — DeepSeek LLM: Scaling Open-Source Language Models with Longtermism. DeepSeek-AI. arXiv:2401.02954, January 2024.

  2. DeepSeekMoE — DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models. Damai Dai, Chengqi Deng, Chenggang Zhao, et al. arXiv:2401.06066, January 2024.

  3. DeepSeek-V2 — DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model. DeepSeek-AI. arXiv:2405.04434, May 2024.

  4. DeepSeek-V3 — DeepSeek-V3 Technical Report. DeepSeek-AI. arXiv:2412.19437, December 2024.

  5. DeepSeek-V3.2 — DeepSeek-V3.2: Pushing the Frontier of Open Large Language Models. DeepSeek-AI. arXiv:2512.02556, December 2025.

  6. DeepSeek-Coder — DeepSeek-Coder: When the Large Language Model Meets Programming — The Rise of Code Intelligence. Daya Guo, Qihao Zhu, Dejian Yang, et al. arXiv:2401.14196, January 2024.

  7. DeepSeekMath — DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models. Zhihong Shao, Peiyi Wang, Qihao Zhu, et al. arXiv:2402.03300, February 2024.

  8. DeepSeek-Coder-V2 — DeepSeek-Coder-V2: Breaking the Barrier of Closed-Source Models in Code Intelligence. DeepSeek-AI. arXiv:2406.11931, June 2024.

  9. DeepSeek-Prover — DeepSeek-Prover: Advancing Theorem Proving in LLMs through Large-Scale Synthetic Data. Huajian Xin, Daya Guo, Zhihong Shao, et al. arXiv:2405.14333, May 2024.

  10. DeepSeek-Prover-V1.5 — DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search. Huajian Xin, Z.Z. Ren, Junxiao Song, et al. arXiv:2408.08152, August 2024.

  11. DeepSeek-R1 — DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. DeepSeek-AI. arXiv:2501.12948, January 2025.

  12. DeepSeek-Prover-V2 — DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition. Z.Z. Ren, Zhihong Shao, Junxiao Song, et al. arXiv:2504.21801, April 2025.

  13. DeepSeekMath-V2 — DeepSeekMath-V2: Towards Self-Verifiable Mathematical Reasoning. Zhihong Shao, Yuxiang Luo, Chengda Lu, et al. arXiv:2511.22570, November 2025.